I’ve tried understanding Bayes’ Theorem several times. I’ve always managed to get confused. Specifically, I’ve always wondered why it’s better than simply using the average estimate from the past. So here’s a little attempt to jog my memory the next time I forget.
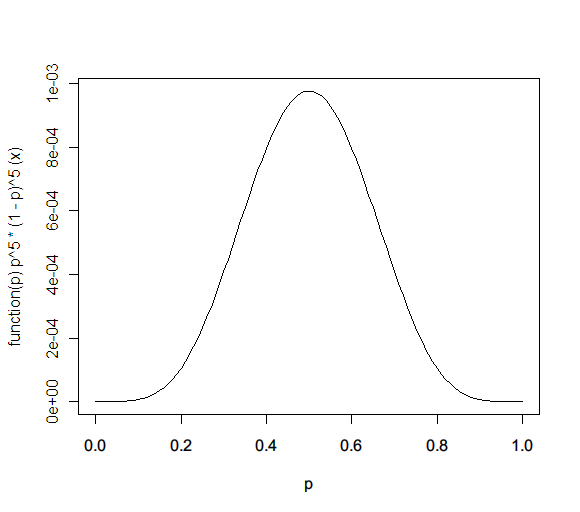
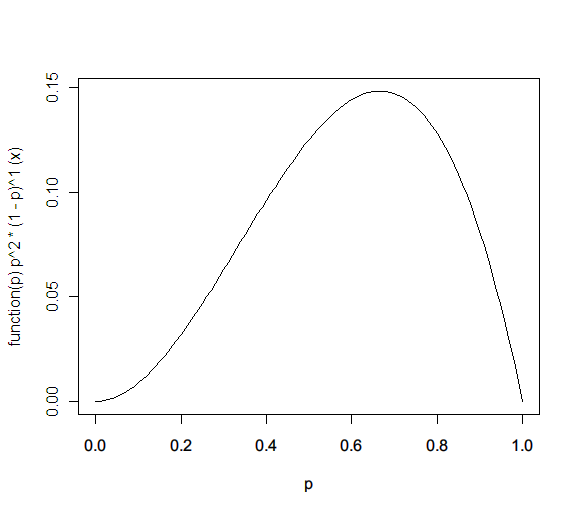
Q: A coin shows 5 heads when tossed 10 times. What’s the probability of a heads?
A: It’s not 0.5. That’s the most likely estimate. The probability distribution is actually:
That’s because you don’t really know the probability with which the coin will throw a heads. It could be any number p. So lets say we have a probability distribution for it, f(p).
Initially, you don’t know what this probability distribution is. So assume they’re all the same – a flat function: f(p) = 1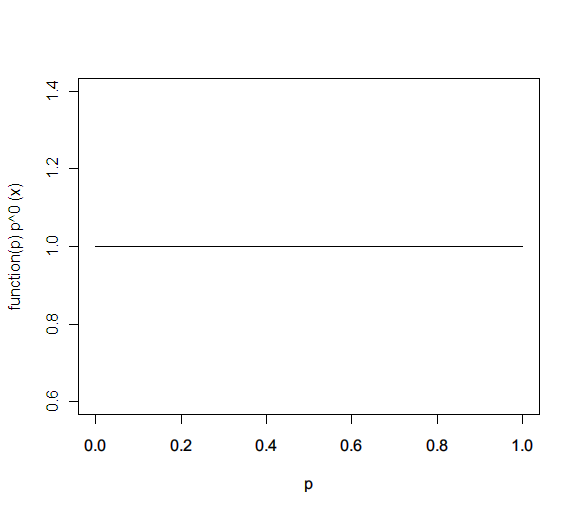
Now, given this, let’s say a heads falls on the next toss. What’s the revised probability distribution? It’s:
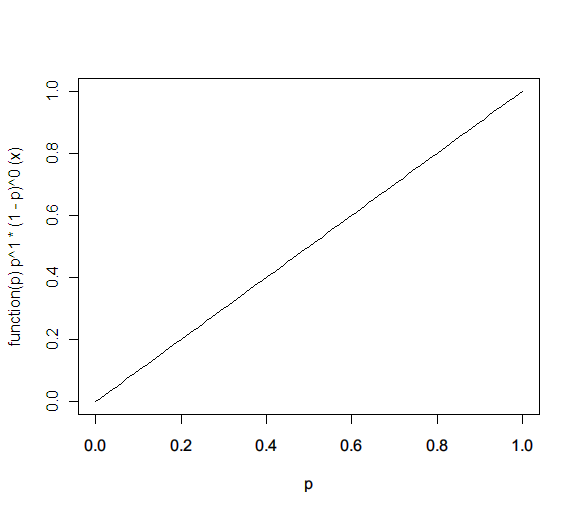
f(p) ← f(p) * probability(heads | x) / probability(heads) = 1 * (x^1 * (1-x)^0) / 1 = x
Let’s say the next is again a heads. Now it’s
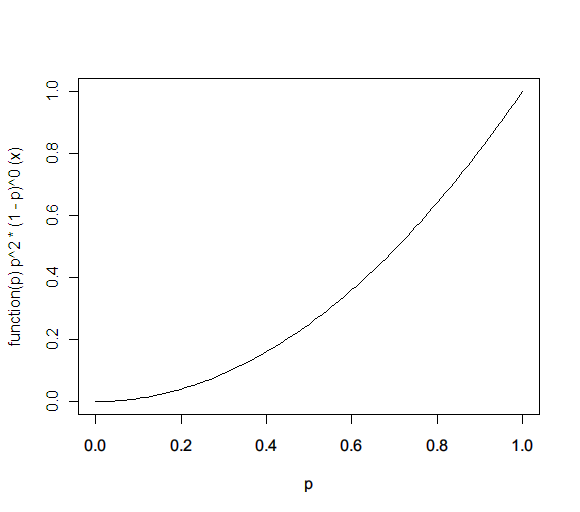
f(p) ← f(p) * probability(heads | x) / probability(heads) = x * (x^1 * (1-x)^0) / 1 = x^2
Now if it’s a tails, it becomes:
f(p) ← f(p) * prob(tails | x) / prob(tails) = x^2 * (x^0 * (1-x)^1) / 1 = x^2 * (1-x)
… and so on. (This happens to be a called a Beta distribution.)
Now, instead of this being the probability of heads, it could be the probability of a person having blood pressure, or a document being spam. As you get more data, the probability distribution of the probability keeps getting revised.
Hi Anand,
f(p) ← f(p) * probability(heads | x) / probability(heads) = 1 * (x^1 * (1-x)^0) / 1 = x
What I understand from the above notation is f(p) stands for probability distribution function (which is used recursively), x stands for the probability of getting a head (which is unknown) and 1-x stands for the complement of x.
Can you please explain why the distribution function is defined as you have done? i.e. , f(p) ← f(p) * probability(heads | x) / probability(heads)